Seismic source inversion is the method of inferring the spatial orientation of an earthquake source from seismic records. The results come with large uncertainties, which we try to estimate with a Bayesian approach. We propose an empirical relationship for a likelihood function based on a large dataset of deterministic solutions. This allows to use the cross-correlation coefficient as a misfit criterion, which is better suited for waveform comparison than the popular root mean square (aka L2-norm).
Feel free to have a look and leave a comment until 25 Jul 2016 at: http://www.solid-earth-discuss.net/se-2016-87/
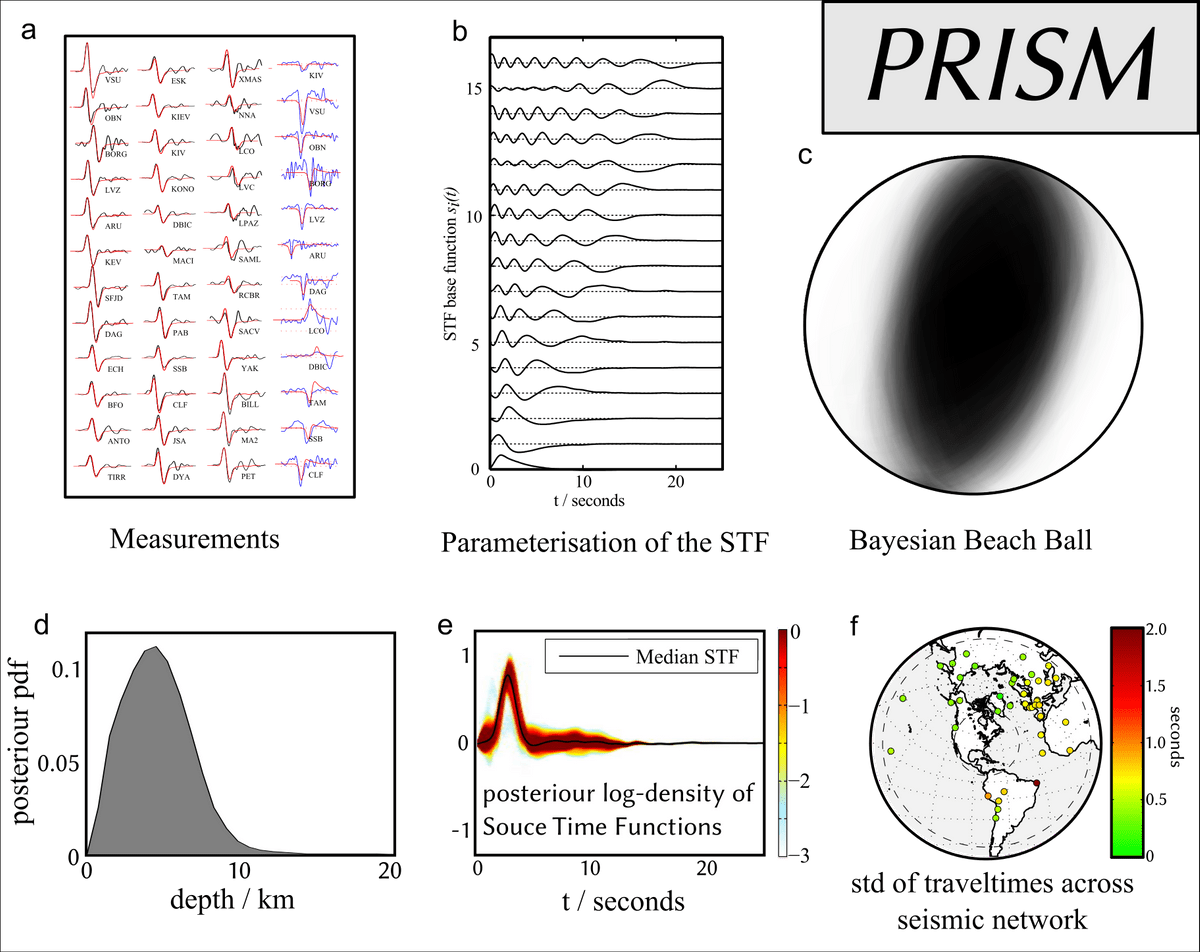
Visual summary of the fully probabilistic source inversion algorithm PRISM presented in the companion paper (Stähler & Sigloch, 2014), on the example of a magnitude 5.7 earthquake in the U.S. state of Virginia on 2011/08/23.
a) Candidate source solutions are evaluated according to the cross-correlation fit they produce between observed broadband, teleseismic P-waveforms (black) or SH-waveforms (blue), and their modeled counterparts (red). The present study is concerned with quantifying the noise distribution on these cross-correlation measurements CC - one scalar per source-receiver pair, 48 in total for this earthquake.
b) To reduce the dimensionality of the model space to a number accessible to Bayesian sampling, the source time function (STF) is parameterised as a linear combination of 15 empirical orthogonal functions found to best span the space of a large set of 900 reference STFs (Sigloch & Nolet, 2006, Stähler et al. 2012).
c) The "Bayesian Beach Ball", a visual average of the posterior ensemble of well-fitting solutions, conveys not only the nature of the moment tensor but also the magnitude and nature of its uncertainties.
d) The marginal probability of the hypocenter depth.
e) Weighted average of STFs from the posterior ensemble of good solutions permits to assess the uncertainties in STF shape. This STF is clearly unimodal and of less than 5 s duration.
f) As a secondary benefit, this procedure yields the uncertainties (standard deviations) of cross-correlation traveltime measurements at all stations, and their inter-station correlations. Traveltimes are the primary input data for seismic tomography and these insights into their uncertainties are not readily available from other methods.
